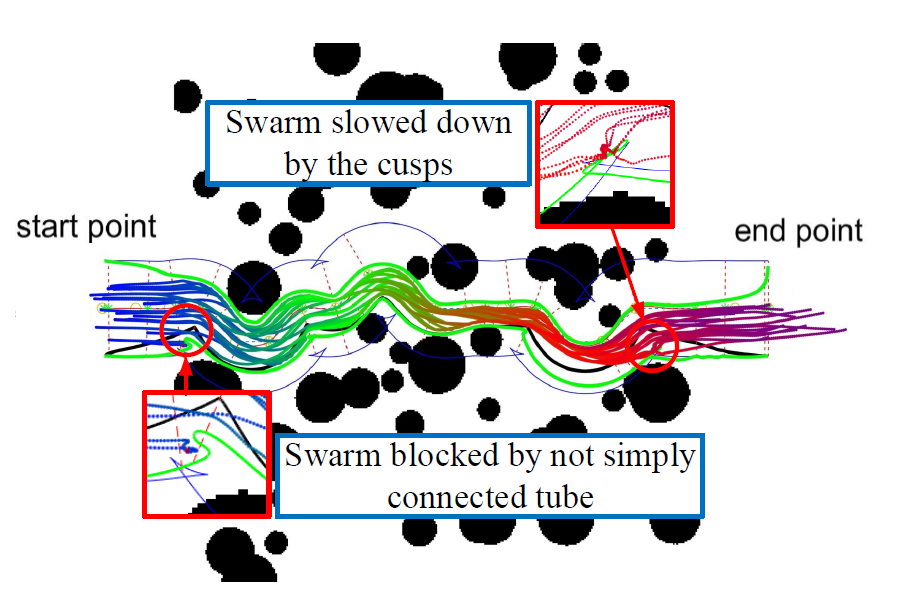
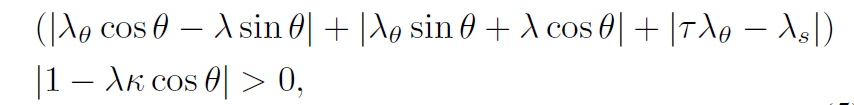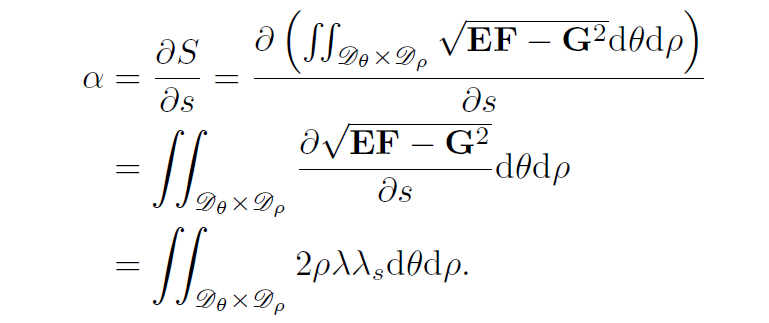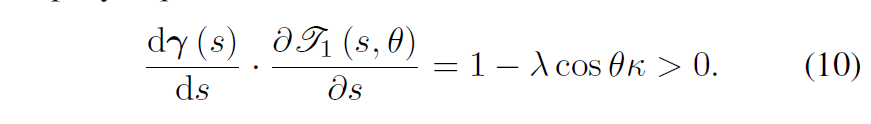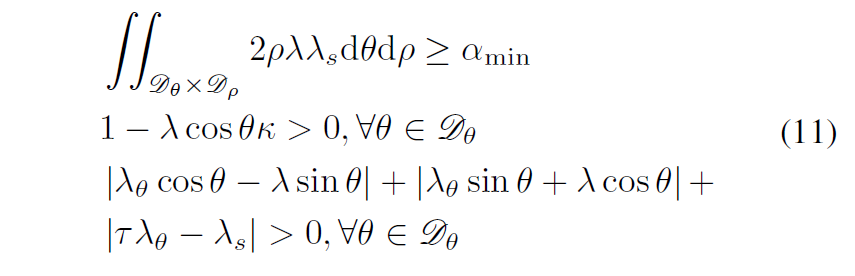无人机集群穿越障碍物环境目前受到越来越多的关注。如何让无人机集群安全流畅地穿越是目前研究地难点和热门领域,目前有仿生算法、轨迹优化等几种技术路线。仿生集群是其中一个研究方向,比较有代表性的是Flocking模型。它基于三个简单的基本原则:排斥相邻个体,与周围个体速度保持一致性,被目标点吸引。其特点为计算量小,与集群数量相关性小,但是容易被非凸障碍物阻滞。而轨迹规划的方法可以生成流畅顺滑的轨迹,但是缺点在于计算量大,随着集群数量的增加其计算量亦增加较大。受这两种方法的启发,提出了一种虚拟管道控制的方法,其中管道由轨迹规划的方法生成,集群由Flocking算法进行虚拟管道内的控制。而本文的目的就是规划出虚拟管道从而为集群控制使用。
01
正则虚拟管道的数学描述
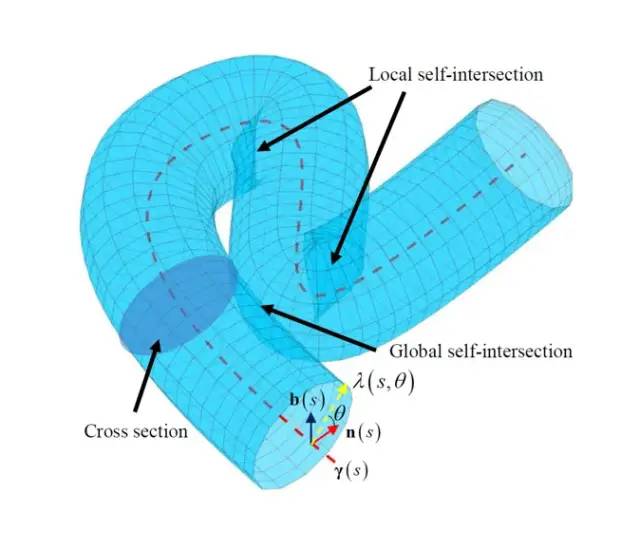
图1 虚拟管道
形象地描述,虚拟管道就是一个横截面沿着一条垂直于它地生成线移动而生成的一片区域,如图1所示。其数学定义如下:
由于虚拟管道的全局或者局部特性,可能会出现自交的情况,因此自交的定义如下:

而自交也分为两种情况分别为局部自交和全局自交,因此需要分别进行定义:

管道的收缩率定义如下:
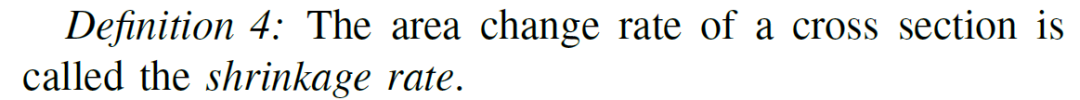
为了更好地理解定义,我们需要了解一些基础知识。表面正则定义为:

单连通定义为:

因为管道的多样性,一些管道特性可能并不适合于集群控制,如图2所示。因此我们需要一种适合与集群飞行的管道,称为正则虚拟管道,其需具备四个性质:
虚拟管道的表面是正则的。
虚拟管道的收缩率是小的。
虚拟管道的截面是单连通的。
虚拟管道无自交。

图2 一些不期望出现的管道特性
综上,正则虚拟管道被定义为:

02
正则虚拟管道的性质
根据之前提出的四个原则,我们分别进行数学的描述,并将其作为约束用于正则虚拟管道的规划中。
原则1:虚拟管道的表面是正则的。
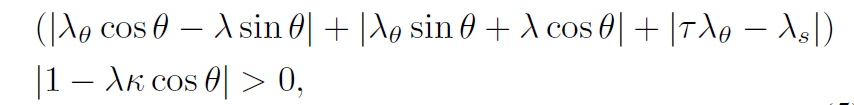
原则2:虚拟管道的收缩率是小的。
收缩率可以数学描述为
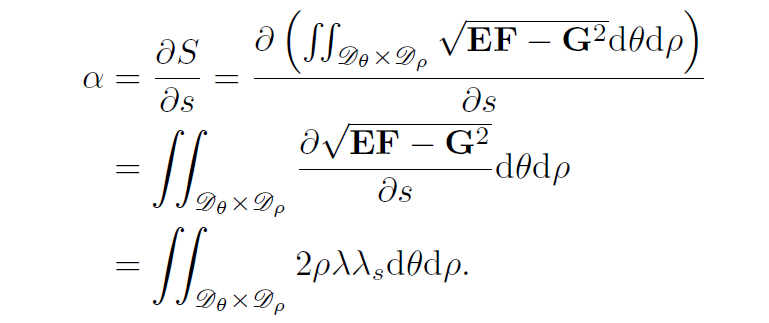
则设定一个收缩率的最大值使得其不得大于这个值。
原则3:虚拟管道的截面是单连通的。
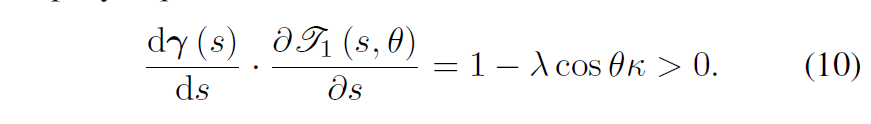
原则4:虚拟管道无自交。
通过观察管道的自交和单连通情况,我们可以证明他们之间的一个明确联系,即若管道是单连通的,则该管道无自交。
综上,四条原则可以写成三条约束如下:
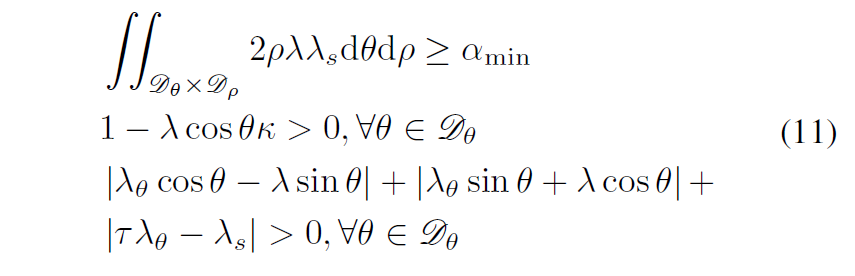
03
正则管道规划方法
正则管道的规划方法可以分为两个部分,分别是生成线规划和管道半径规划。首先进行管道生成线的规划。
01
管道生成线规划
生成线用n阶极点多项式来描述,首先用A*路径搜索算法搜索出一条可通行路径,再将生成线的规划问题转化为一个优化问题,其目标是让曲线更加顺滑。
02
管道半径规划
基于生成线的规划结果,我们将半径的倒数即曲率用n阶极点多项式进行表示,并转化为一个优化问题,目标函数是期望管道空间尽可能得大,约束则包含障碍物约束以及正则约束。其结果如图3所示,绿色线条表示非正则管道的形状,黑色线条表示正则管道的形状。
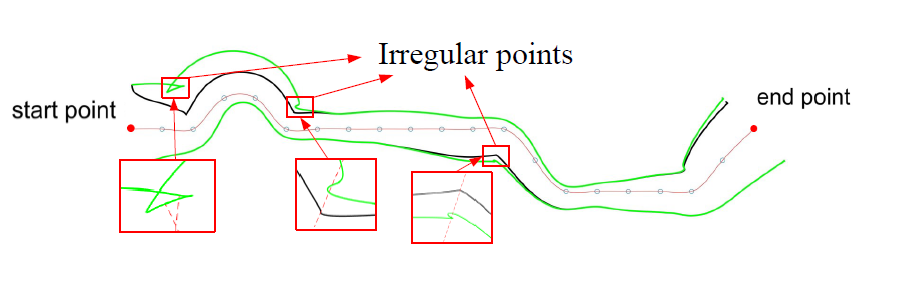
图3 虚拟管道得规划结果
整个过程总结为算法表:

04
仿真结果
我们在MATLAB上实现虚拟管道规划和Flocking集群控制算法的仿真。首先是管道规划的仿真,经过上千次的随机测试,我们验证了正则约束可以有效消除不期望的点的出现,尽管管道的空间缩小了。然后我们进行了无管道、非正则管道、正则管道情况下利用Flocking算法在相同障碍物环境和相同起止点情况下的对比仿真,其结果如下:
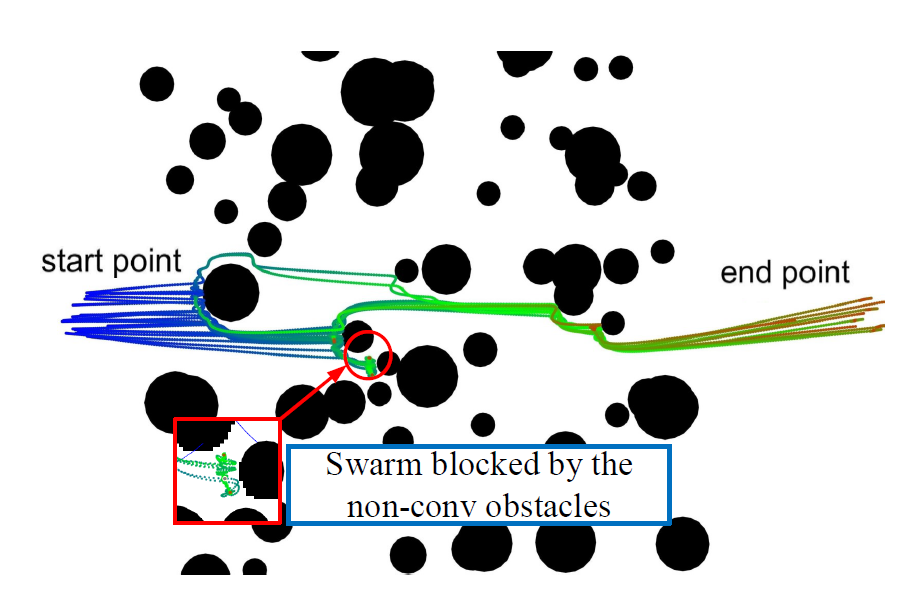
无管道情况
非正则管道情况
正则管道情况
可以看到只有正则管道中集群飞行不会被障碍物或者管道阻滞,可以顺利到达终点,并且经过实验验证,正则管道的飞行时间最短,达到了期望的效果,证明了正则管道的有效。
05
结论
本文我们提出了正则虚拟管道的定义以及规划方法,这种管道适用于Flocking算法的飞行。对比仿真验证了这个方法的有效性。在未来的工作中,将会进行三维的管道规划和实际的飞行试验。